The Wave: Part 1
This is the first of many little itty-bitty dives into one part of the app. Today its the wave.


I'll include the general design philosophy in another article. There, it will be made clearer why the wave exists.
Karen from the TV show spongebob (left), has a simple green wave that morphs and animates alongside her speech that I've recreated for this project(right). Here is the technical breakdown.
Lets say you have a song, and you want to determine what notes make it up. We have the technology! It is called the Fourier Transform and is one of the most powerful tools math has to offer engineers. Broadly speaking, it takes complex sounds, like speech and puts them in terms of their underlying frequency components. ooo... shiny.
When we speak, our vocal cords vibrate to produce a complex waveform that contains a mixture of different frequencies. The Fourier transform breaks down this complex speech waveform into its component sine and cosine waves of different frequencies, amplitudes, and phases. This frequency-domain representation reveals the individual phonemes that make up speech.
Each phoneme has a characteristic frequency "signature" that the Fourier transform can pick up on. For example, the vowel sounds like "s" have higher frequency profiles than "oo" and "aa". The resultant chart is a distribution of audio signals with a x axis being the frequency and the y axis being the strength that given frequency.
To get the look I want, distribution needs 2 additional transformations. The samples are first rearranged such that higher pitches land on the left and right while lower ones tend towards the middle. Each sample has an index, [1,2,3,4,5,6,7,8... 32], which becomes [31,29...5,3,1,2,4...30,32]. Then, every other index is multiplied by -1 to get it underneath the horizontal axis. This last step is responsible for the zigzag of the line.
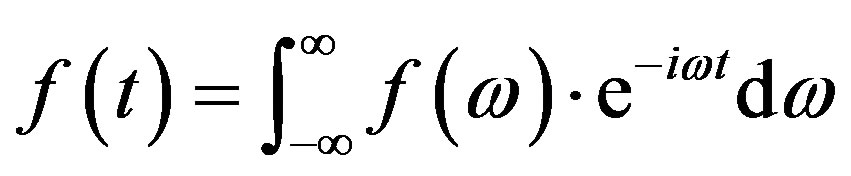


Very impressive, Owen. I look forward to seeing how this all plays out but sounds like you have a great start to understanding the process.
ReplyDelete